Mahalanobis距离 | BigflyのBlog

知识储备：

协方差概念
欧几里得距离（欧氏距离）
线性代数
PCA算法

一、前言：

在学习deepsort相关内容，提到了马氏距离，之前也有所耳闻，但没有深入了解，只是知道它是度量学习中一种常用的距离指标，同欧氏距离、曼哈顿距离、汉明距离等一样被用作评定数据之间相似度的一种指标。查阅了很多博主写的相关文章，似乎没有讲到本质的地方且对新手不太友好，借此机会对其原理以及方法进行了详细了解，并用笔者的思路来为大家进行讲解。

二、概念：

三、解释

以上是维基百科给出的解释，看到这你是不是懵逼了，没关系且听我细说。

大话概念：马氏距离是一种测量两个点之间距离的方法，不同于欧几里得距离，它考虑了数据的协方差。这使得马氏距离能有效得度量在多维空间中的距离，尤其是对用不同维度之间存在相关性的数据。

四、欧氏距离与马氏距离

4.1 单变量欧氏距离

如下图，假设圆圈表示数据样本，数据的均值为0，那么欧式距离就是圆圈离0的远近。

图1

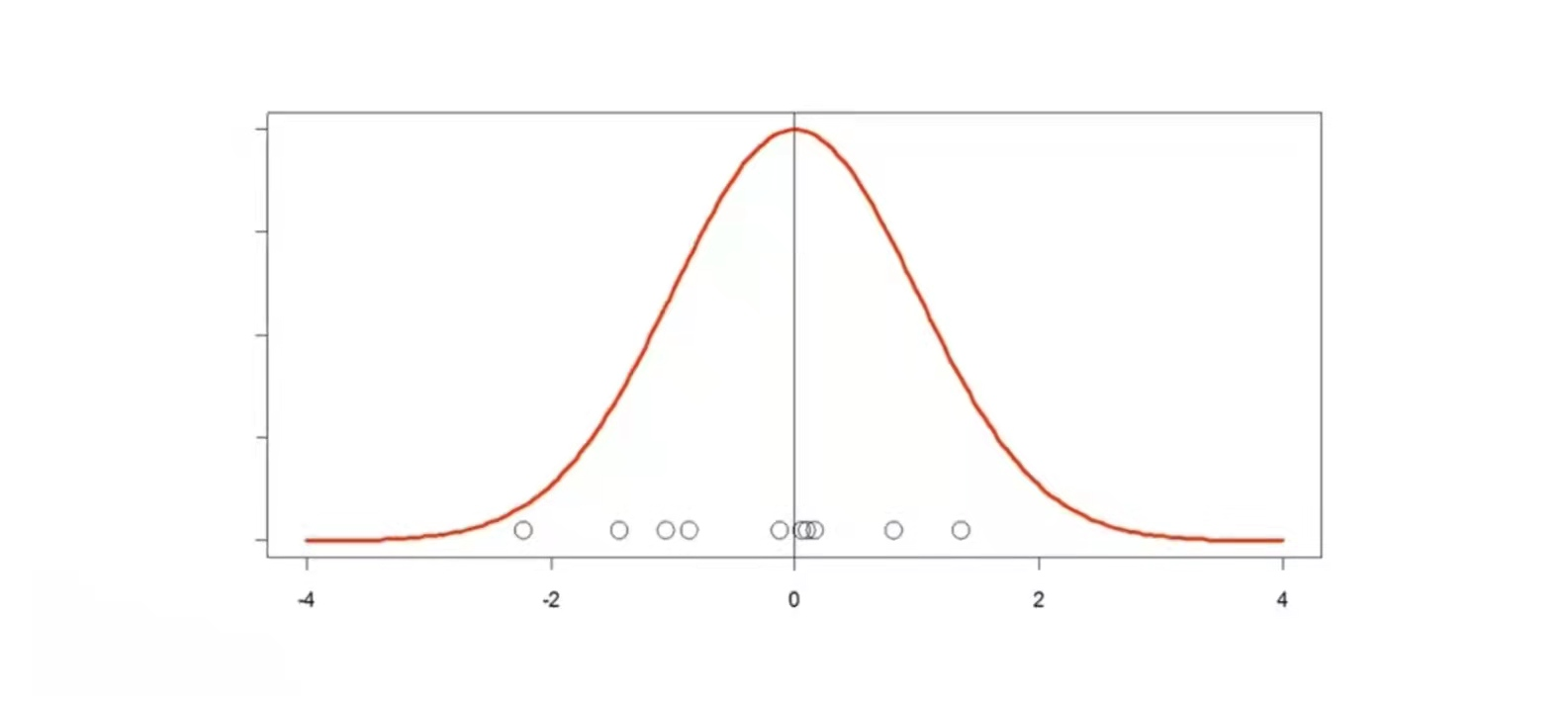
4.2 多变量欧氏距离

图2为高维空间中数据点在平面上的投影图中的红色➕表示数据点的均值点，点i（任意数据点）与均值点之间的欧氏距离可通过如下公式计算得到。

图2

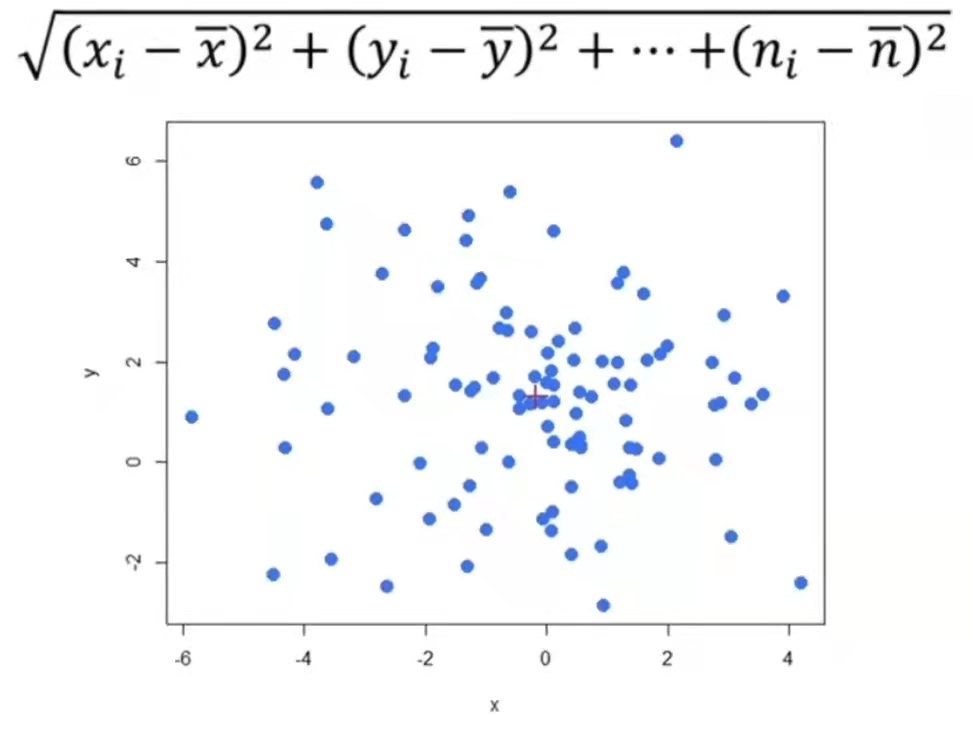
4.3欧氏距离的局限性

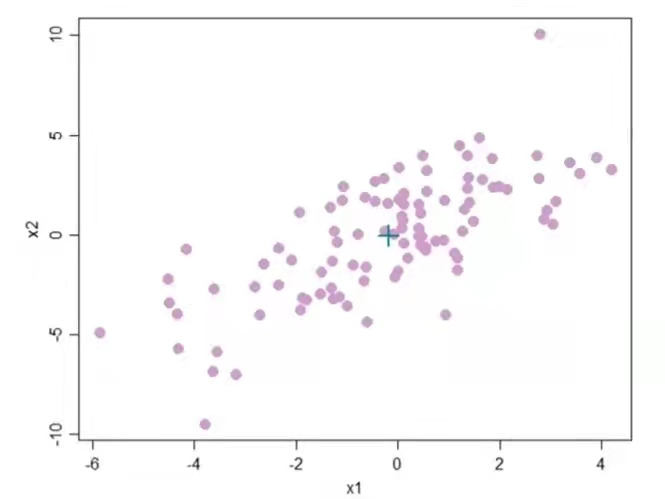
如图3所示若数据样本之间存在协方差，那么欧式距离就不太适用。例如图中的红色方块和蓝色方块距离均值点 ➕的欧式距离是相等的。直观的看红色方块是一个异常点（离群点），此时若用欧几里得距离作为度量距离的指标显然不太适合。

图3

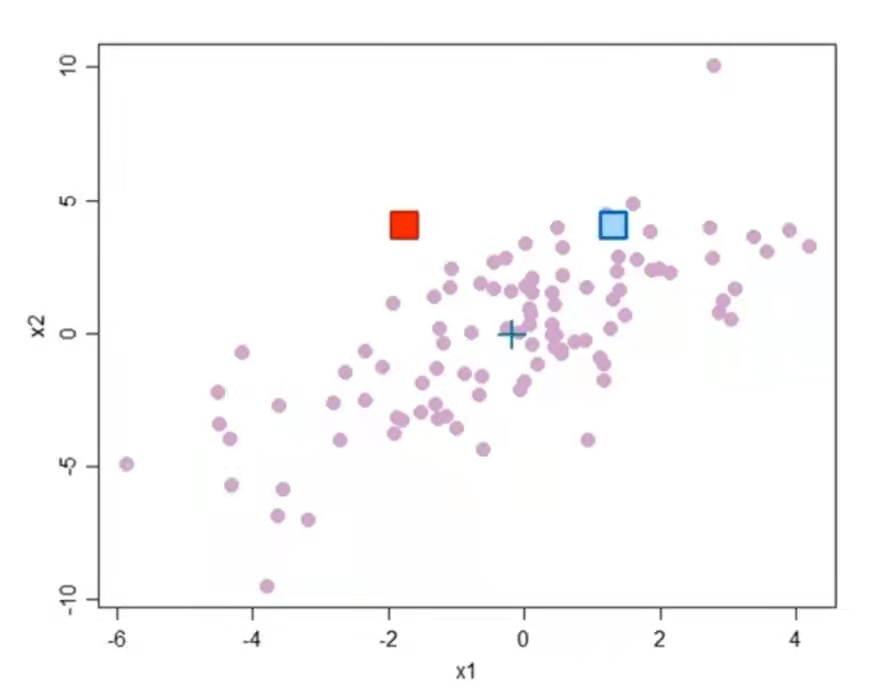
4.4马氏距离

协方差：

$$
Cov(X,Y) = E((X-E[X])(Y-E[Y]))
= E(XY)-2E(X)E(Y)-E(X)E(Y)
= E(XY)-E(X)E(Y)
$$

对于上述公式中E表示求均值，对于第一行若有Y=X则Cov(X,Y) = E((X-E[X])(Y-E[Y]))=(X-E[X])(X-E[X])=var(X),即一个变量与自身的协方差等于方差，记住这一点后面会用到。

所有变量对的协方差矩阵如下图所示：

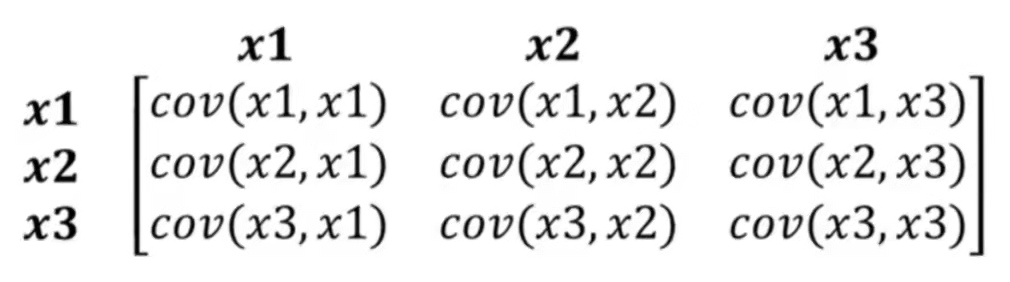
协方差矩阵是一个方阵，这里展示的是一个3x3的协方差矩阵，它包含所有变量对之间的协方差。

基于以下两点我们可以对上面的协方差矩阵进行变形,变形结果如下所示。

一个变量X与自身的协方差也就是方差，这一点在前面推导有提到过，在此不再赘述。
协方差满足交换律即cov(x1,x2)=cov(x2,x1)

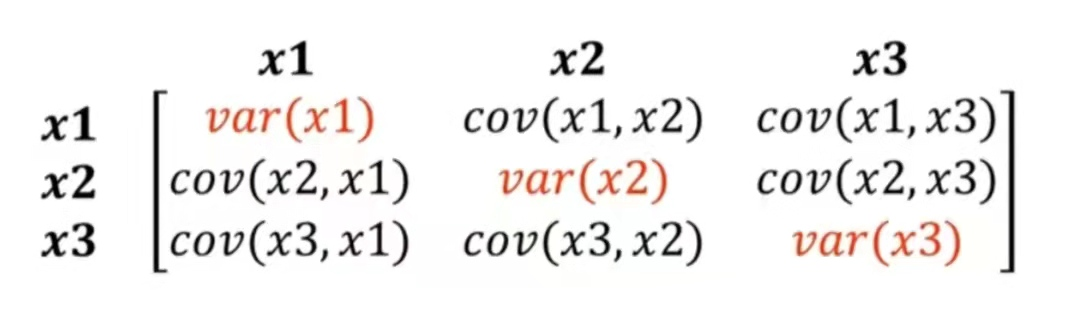
上述矩阵是一个实对称矩阵。且在主斜对角线上面的值都是方差，这也就是协方差矩阵名称的来源。

回到欧几里得距离的问题，如果我们能以某种方式，重新缩放图4，使得变量之间不再具有其协方差，它会鲁棒性更强，这就是马氏距离要解决的问题，了解这一点我认为是至关重要的，很多很多博主都讲马氏距离、协方差、讲的没错，但没有刨根问题，究其本质。后面笔者将讲述如何对其进行Rescaling to Remove Covariance,也就是去协方差。

图4

Rescaling to Remove Covariance：

首先讲这个问题之前我们先来回顾一个表达式Ax=λx,也就是特征值与特征向量之间的关系。举一个简单的例子：

这是一个2x2的矩阵：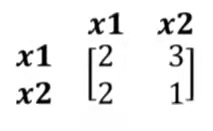

N维矩阵有N个特征向量，且不同特征向量相互正交，这里笔者举例的特征向量是二维的，所以其有两个相互正交的特征向量，我们找到其一个特征向量，通过Ax=λx构造如下表达式：

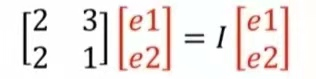
所以我们就可以根据线性代数的知识求出特征值I和特征向量x（也就是Ax=λx中的λ和x）。对图3中的数据求其协方差矩阵对应特征向量、特征值，结果如图5所示。

图5

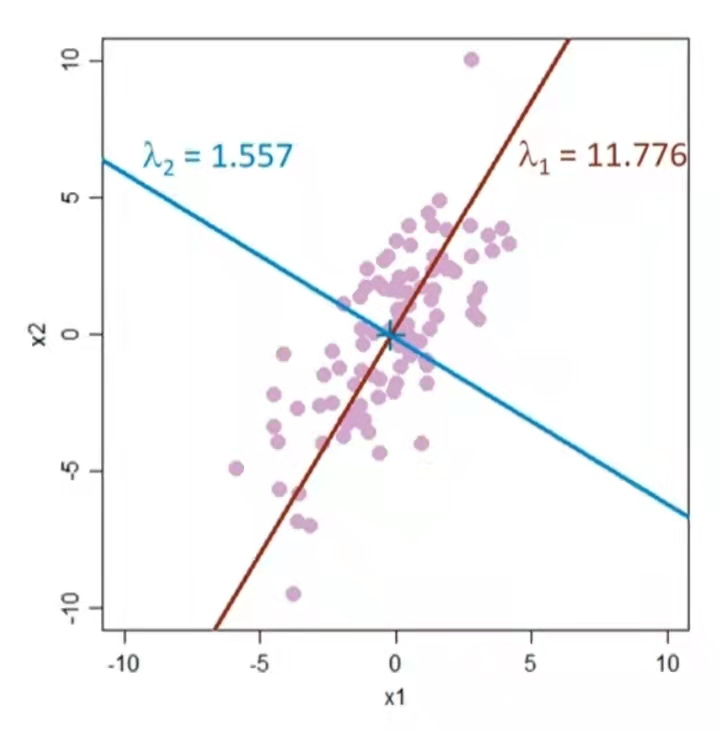
提示：有小伙伴可能好奇特征向量是如何求出的，这里笔者不进行详细讲解，这是线性代数的相关内容。但给出一些结论。首先最大特征向量与数据最大方向差方向一致，如上图中红色直线所指，，其次特征向量是相互正交的，且第二特征向量是与第一特征向量垂直的方向上数据方向差最大的方向，以此类推可以求出所有特征向量

得到特征向量之后，以特征向量为坐标轴对数据点进行旋转变换，并且对数据点进行尺度压缩，也就是对特征向量所在坐标轴的尺度除以其特征值的平方根，这样特征值大的坐标轴被压缩的尺度也就相应的大一些。

图6

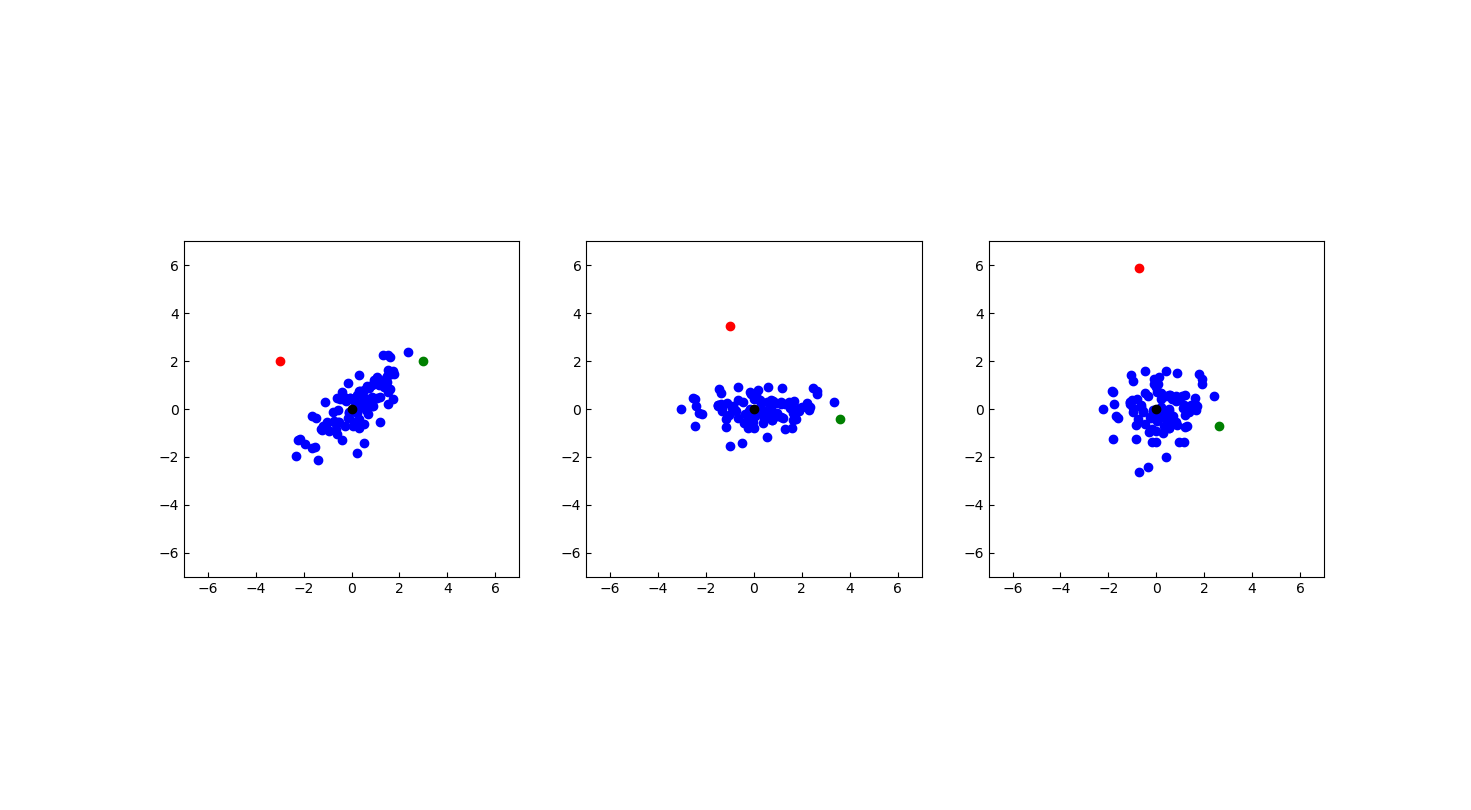
如上图所示作图为原始的数据点，其中红点与绿点距离距离均值点（黑点）的欧几里得距离是相等的，可以对其进行坐标轴旋转，得到中间的数据分布，之后对其进行数据压缩可以得到有图所示的点，如此就可以过滤掉离群点，也就是其中的红点。

绘制代码如下：

from scipy.spatial.distance import pdist
from numpy import array, cov, diag, mean, sqrt, vstack
from numpy.random import multivariate_normal
from numpy.linalg import eig
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt


"""生成二维正太分布数据`X` 两个维度间的协方差为0.8(强相关).
在X的尾部加入点A和点B,点B属于数据集X而点A为异常点,且点A和B到原点(0,0)的`欧式距离`相等.
本次实验旨在通过坐标旋转和缩放后通过欧式距离将点A和B区分开,理解马氏距离中sigma的物理意义."""

N = 100  # 数据集大小
X = multivariate_normal(mean=[0, 0],size=N,cov=[[1, 0.8],[0.8, 1]])
point_A = array([-3, 2])  # 异常点
point_B = array([3, 2])# 添加点A和B到尾部
X = vstack((X, point_A))
X = vstack((X, point_B))# 旋转
Q, U = eig(cov(X, rowvar=False))
Y = X.dot(U)
# 缩放
Cov_Y = cov(Y, rowvar=False)  # 求Y的协方差矩阵
diag_Y = diag([sqrt(1/Cov_Y[i][i]) for i in range(len(Cov_Y))])  # 取协方差矩阵对角线元素的倒数
Z = Y.dot(diag_Y)  # 缩放后的特征print(pdist(X, 'mahalanobis')) # 原始数据X的马氏距离
print(pdist(Z)) # 旋转缩放后的欧氏距离
def plot_point(data, N, plt_temp):
    plt_temp.scatter(data[:N, 0], data[:N, 1], c='b')
    plt_temp.scatter(data[N, 0], data[N, 1], c='r')  # 点A
    plt_temp.scatter(data[N+1, 0], data[N+1, 1], c='g')
    plt_temp.scatter(0, 0, c='k')  # 原点

    plt.axis('square')
    plt_temp.xlim([-7, 7])
    plt_temp.ylim([-7, 7])
    return plt_temp

plt.rcParams['xtick.direction']= 'in'
plt.rcParams['ytick.direction']= 'in'

plt.subplot(1, 3, 1)

plt = plot_point(X, N, plt)
plt.subplot(1, 3, 2)
plt = plot_point(Y, N, plt)
plt.subplot(1, 3, 3)
plt = plot_point(Z, N, plt)
plt.show()

用公式表示如图7，其中S为协方差矩阵，协方差矩的逆阵左乘均值的转置并右乘均值，就得到马氏距离的平方，当协方差为单位阵那么马氏距离就可以简化为欧氏距离。

图7

这里的核心思想就是，如果数据在某个方向上变化较大，那么在这个方向上的单位距离就应该被“缩短”，而如果数据在某个方向上变化较小，那么这个方向上的单位距离就应该被‘拉长“，这就是协方差矩阵所起的作用。

六、总结

马氏距离的步骤结论：

将含义协方差的数据分布转换为没有协方差的数据分布，使得数据的鲁棒性更强；
使得他们的方差为1；
计算变换后数据分布的欧几里得距离即为马氏距离。

与欧氏距离不同的是，马氏距离考虑了各种特性之间的联系（例如：一条关于身高的信息会带来一条关于体重的信息，因为这两者之间是有一定的关联的），并且尺度无关的（scale-invariant），即独立于测量尺度。

一句话总结：马氏距离通过将数据进行坐标旋转，并缩放到另一个空间后可以直接使用欧式距离，进而过滤掉在欧氏距离中无法过滤的离群点。